Задачи по микроэкономике. Часть 12 (потребительский выбор)

Задача №1733 (линия бюджетного ограничения)

Второклассник Антон тратит все свои карманные деньги на мороженое и лимонад. Изобразите на графике линию бюджетного ограничения Антона за неделю, если за это время родители выдают ему 120 рублей, при этом одно мороженое стоит 20 рублей, а баночка лимонада стоит 30 рублей. Как изменится бюджетная линия, если цена мороженого также повысится до 30 рублей? Изобразите соответствующее изменение на графике.

Решение задачи:

Бюджетная линия – это геометрическое место точек, характеризующих все наборы товаров, которые может приобрести потребитель, полностью израсходовав свой доход Д при данных ценах товаров Рх и Ру.

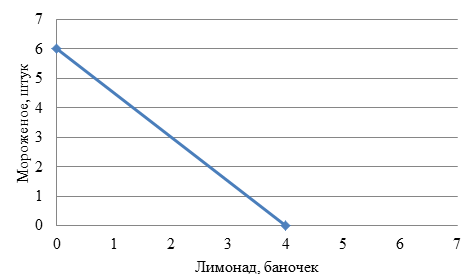
Доход Антона составляет 120 руб. Этот доход можно потратить на приобретение 6-ти штук (120/20) мороженого по цене 20 руб. или 4-х баночек лимонада (120/30) по цене 30 руб. Используя эти данные, строим линию бюджетного ограничения Антона:

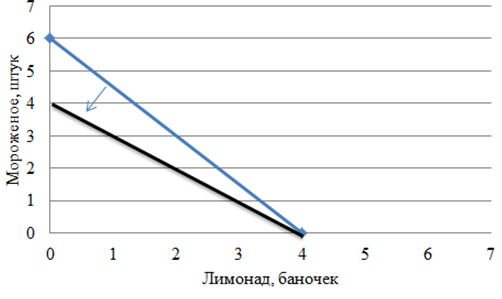
Если же цена мороженого увеличится до 30 руб., то Антон сможет купить не 6 штук мороженого, а только 4 штуки. Бюджетная линия изменится следующим образом:

Обновить  

 
# Задача №9922 (потребительское поведение) — Администратор 22.08.2023 17:29
Известно, что для потребительского набора (x, y) функция полезности потребителя задана уравнением

Общий доход, которым располагает потребитель, составляет m=240. Цена товара x – Px=4 ден. ед., цена товара y – py1=10 ден. ед. Предположим, что цена товара y снижается до уровня py2=5.
Осуществите следующие действия:
- выпишите уравнение бюджетной линии и постройте график бюджетного ограничения;
- определите эффект замены (по Хиксу);
- определите эффект дохода (по Хиксу);
- определите общий эффект (по Хиксу);
- охарактеризуйте данный товар (нормальный, инфериорный, товар Гиффена).
Перейти к демонстрационной версии решения задачи
 
 
# Задача №9921 (бюджетное ограничение и бюджетное множество) — Администратор 22.08.2023 17:29
Предположим, что доход потребителя в месяц составляет m=3000 руб. на потребительский набор (x, y). Цена единицы товара x равна px=60 руб., а цена единицы товара y равна py=40 руб.
1. Запишите бюджетное ограничение (БО) потребителя и покажите на графике соответствующее бюджетное множество (БМ).
2. Изменения в экономике привели к необходимости ввести налог на цену товара x. Теперь каждая единица товара x будет обходиться всем потребителям на 10% дороже. Запишите БО для этого случая и покажите на графике соответствующее БМ. Ответьте на вопрос: что произошло со множеством доступных потребителю наборов после ограничительной политики правительства?
3. В результате введения правительством налога на цену товара администрацией региона была введена потоварная субсидия на товар y, равная сумме s=12 руб. Запишите БО для этого случая и покажите графически БМ. Как изменилось бюджетное множество потребителя по сравнению с начальным вариантом?
4. Все правительственные программы отменены (т.е. пункты 2 и 3). Магазин, в котором потребитель совершает свои покупки, вводит в действие следующую систему скидок: при покупке товара y все приобретенные единицы продаются на S=2 руб. дешевле. Выпишите БО и покажите на графике соответствующее БМ.
Перейти к демонстрационной версии решения задачи
 
 
# Задача №9705 (потребительское поведение) — Администратор 22.08.2023 11:17
Известно, что для потребительского набора (x, y) функция полезности потребителя задана уравнением

Общий доход, которым располагает потребитель, составляет m=360. Цена товара x – px=6 ден. ед., цена товара y – py=4 ден. ед. Предположим, что цена товара y снижается до уровня py2=2.
Осуществите следующие действия:
- выпишите уравнение бюджетной линии и постройте график бюджетного ограничения;
- определите эффект замены (по Хиксу);
- определите эффект дохода (по Хиксу);
- определите общий эффект (по Хиксу);
- охарактеризуйте данный товар (нормальный, инфериорный, товар Гиффена).
Перейти к демонстрационной версии решения задачи
 
 
# Задача №9704 (бюджетное ограничение и бюджетное множество) — Администратор 22.08.2023 11:17
Предположим, что доход потребителя в месяц составляет m=7000 руб. на потребительский набор (x, y). Цена единицы товара x равна px=70 руб., а цена единицы товара y равна py=50 руб.
1. Запишите бюджетное ограничение (БО) потребителя и покажите на графике соответствующее бюджетное множество (БМ).
2. Изменения в экономике привели к необходимости ввести налог на цену товара x. Теперь каждая единица товара x будет обходиться всем потребителям на 10% дороже. Запишите БО для этого случая и покажите на графике соответствующее БМ. Ответьте на вопрос: что произошло со множеством доступных потребителю наборов после ограничительной политики правительства?
3. В результате введения правительством налога на цену товара администрацией региона была введена потоварная субсидия на товар y, равная сумме s=5 руб. Запишите БО для этого случая и покажите графически БМ. Как изменилось бюджетное множество потребителя по сравнению с начальным вариантом?
4. Все правительственные программы отменены (т.е. пункты 2 и 3). Магазин, в котором потребитель совершает свои покупки, вводит в действие следующую систему скидок: при покупке товара y все приобретенные единицы продаются на S=5 руб. дешевле. Выпишите БО и покажите на графике соответствующее БМ.
Перейти к демонстрационной версии решения задачи
 
 
# Задача №9697 (потребительское поведение) — Администратор 22.08.2023 11:11
Известно, что для потребительского набора (x, y) ункция полезности потребителя задана уравнением u(x, y)=4*x*y. Общий доход, которым располагает потребитель, составляет m=480. Цена товара x – px=2 ден. ед., цена товара y – py1=6 ден. ед. Предположим, что цена товара y увеличивается до уровня py2=8.
Осуществите следующие действия:
- выпишите уравнение бюджетной линии и постройте график бюджетного ограничения;
- определите эффект замены (по Хиксу);
- определите эффект дохода (по Хиксу);
- определите общий эффект (по Хиксу);
- охарактеризуйте данный товар (нормальный, инфериорный, товар Гиффена).
Перейти к демонстрационной версии решения задачи
 
 
# Задача №9696 (бюджетное ограничение и бюджетное множество) — Администратор 22.08.2023 11:10
Предположим, что доход потребителя в месяц составляет m=8000 руб. на потребительский набор (x, y). Цена единицы товара x равна px=100 руб., а цена единицы товара y равна py=200 руб.
1. Запишите бюджетное ограничение (БО) потребителя и покажите на графике соответствующее бюджетное множество (БМ).
2. Изменения в экономике привели к необходимости ввести налог на цену товара x. Теперь каждая единица товара x будет обходиться всем потребителям на 20% дороже. Запишите БО для этого случая и покажите на графике соответствующее БМ. Ответьте на вопрос: что произошло со множеством доступных потребителю наборов после ограничительной политики правительства?
3. В результате введения правительством налога на цену товара администрацией региона была введена потоварная субсидия на товар y, равная сумме s=20 руб. Запишите БО для этого случая и покажите графически БМ. Как изменилось бюджетное множество потребителя по сравнению с начальным вариантом?
4. Все правительственные программы отменены (т.е. пункты 2 и 3). Магазин, в котором потребитель совершает свои покупки, вводит в действие следующую систему скидок: при покупке товара y все приобретенные единицы продаются на S=30 руб. дешевле. Выпишите БО и покажите на графике соответствующее БМ.
Перейти к демонстрационной версии решения задачи
 
 
# Задача №5690 (бюджетная линия) — Администратор 10.07.2018 17:15
Дана бюджетная функция: (Р1*, Р2* – цены после изменения)

Построить бюджетную линию до и после изменения цен; рассчитать и отметить на графиках точки оптимума; найти эффект замены и эффект дохода.
Перейти к демонстрационной версии решения задачи
 
 
# Задача №4891 (кривая безразличия и бюджетная линия) — Администратор 11.08.2017 10:23
На рисунке показана одна из кривых безразличия некоего потребителя и его бюджетная линия. Цена товара У равна 12 руб.
а) Каков доход потребителя?
б) Какова цена товара Х?
в) Как изменится положение бюджетной линии при увеличении товара У до 15 руб.? снижении до 10 руб.?
г) Напишите уравнение бюджетной линии.

Перейти к демонстрационной версии решения задачи
 
 
# Задача №4880 (оптимальный потребительский набор) — Администратор 11.08.2017 10:07
Предпочтения потребителя заданы в виде функции полезности:

где x1 и x2 – объемы потребления 1-го и 2-го товаров, соответственно.
Доход равен 10 ден.ед. Цены 1-го и 2-го товаров, соответственно, равны: p1=1, p2=2. Найти оптимальный потребительский набор товаров.
Перейти к демонстрационной версии решения задачи
 
 
# Задача №1736 (карта кривых безразличия и бюджетная линия) — Администратор 18.10.2016 21:27
Студент читает журналы и слушает музыку на дисках. Изобразите графически карту кривых безразличия (достаточно трех) и линию бюджетного ограничения. Укажите следующие точки:
а) точку, в которой студент максимально удовлетворяет свои потребности при заданном бюджетном ограничении;
б) точку такого набора, выбрав который, студент не израсходовал бы весь свой доход, предназначенный на покупку указанных товаров;
в) точку, в которой студент получает то же удовлетворение, что и в точке максимизации полезности, но при этом выходит за пределы своих бюджетных возможностей.
Перейти к демонстрационной версии решения задачи
 
 
# Задача №1735 (бюджетная линия потребителя) — Администратор 18.10.2016 21:27
Ученица пятого класса тратит все свои карманные деньги на журналы и пирожки. Изобразите на графике её линию бюджетного ограничения за неделю, если за это время родители выдают ей 100 рублей, при этом один журнал стоит 20 рублей, а один пирожок стоит 25 рублей. Как изменится бюджетная линия, если родители станут давать девочке в неделю 200 рублей? Изобразите соответствующее изменение на графике.
Перейти к демонстрационной версии решения задачи